弧长法基本原理

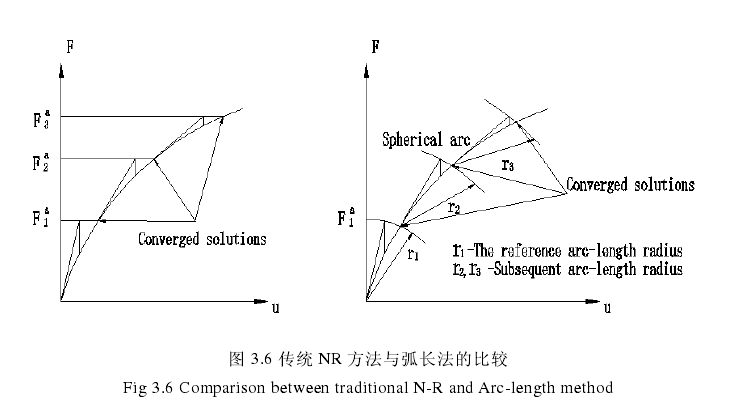
为对结构进行全过程的非线性跟踪分析，了解结构的失稳破坏过程，必须求解得到结构荷载位移曲线的下降段。但是如前文所述：常用的 NR 方法不能求解结构刚度矩阵为负定的情况。近几时年来，国内外许多学者致力于非线性过程跟踪技术的研究提出了许多数值计算方法，目前主要有：人工弹簧法[
27]、位移控制法[28]、弧长法[29, 30]、功控制法[31]、最小余量位移法[32]和当前刚度参数法[33, 34]，其中文献提出的改进后的弧长法[29,  30]，其基本思想在于将参数作为独立变量，在每个荷载增量中进行平衡迭代，在过程中自动控制荷载因子的值，增加约束条件，不同的弧长法的区别在于约束条件的不同。  在求解过程中不管是采取荷载控制还是位移控制，非线性静力平衡方程为：  其中，u 是位移向量， 是荷载控制参数，q 是与位移向量 u 相关的结构内荷载向量，eqp 是固定参考荷载向量。若参数  可以自动增长，即采用荷载控制技术，在极值点附近由上式 3-6 确定平衡路径，与代表外荷载水平的平面 等于常数不相交。由 Riks 和 Wempner 等[35]提出的弧长法就是要找到平衡路径和曲面 s=constant的交点，其中 s 为弧长，其表达式为  其中的大小跟荷载与变形的比例有关。在引入弧长后，使用高阶 ODE 法及预测修正技术直接求解方程  将牛顿法与修正的牛顿法的切线增量预测作为修正技术，从而弧长法可以改写为以下积分形式：  其中 l 是到理想交点的弧长，增量u 和 与上一个收敛平衡状态有关。 弧长法的实质是将荷载参数 为变量，假定结构自由度为 n,整个方程共有 n+1个变量，除了 3-6 中的 n 个方程，还需要一个常量方程 3-9，至此，可以利用牛顿方法求解，整个方程组可以写成：  以上为弧长法的基本原理，由增量形式的不同，弧长法可以分为线性弧长法，球面弧长法，柱面弧长法等等，在各类弧长法中，球面弧长法对结构进行稳定性分析时是最有效的。