非线性稳定
在工程中很多问题都可以忽略一些次要因素,将其简化为线性问题来进行处理,这种情况下需要保证其平衡方程是不依赖变形状态的线性方程;几何方程的应变和位移的关系是线性的;物理方程的应力和应变的关系是线性的;边界上的力和位移也是线性的。但是实际情况中仍然有很大一部分问题不满足上诉条件,
即不能由线性分析解决而必须应用非线性理论才能得到符合实际情况的结果。根据上诉条件的具体特点,非线性问题可以分为以下几类[21, 23]:
①材料非线性问题:所谓材料非线性是指材料的物理规律是非线性的,包括非线性弹性和弹塑性问题,这两者的主要区别在于卸载的过程是否可逆,即材料的变形能否完全恢复。ANSYS 在考虑材料非线性问题时,需要使用者定义的是屈服准则(Von Mises 屈服准则;Hill 屈服准则;Druck-Prager 屈服准则等等)、流动
准则、强化准则(双线性随动强化 BKIN、双线性等向强化 BISO、多线性随动强化 MKIN、多线性等向强化 MISO)。
②几何非线性问题:几何非线性问题指的是在大变形下应变位移关系不再是线性的,结构在荷载的作用下发生大的位移和转动,此时材料还有可能处于线弹性状态,但结构的平衡方程不能再简化为线性形式,必须包含位移的二次项甚至更高次项。ANSYS 中包含有四种几何非线性效应:大位移小应变;大位移大应变;应力刚化;旋转软化。
③边界非线性问题:例如两个物体间的接触和碰撞。 本文的非线性稳定分析主要是指结构的几何非线性问题和材料非线性问题。 在 ANSYS 中非线性稳定分析中是采用逐渐增加荷载的方法来求得结构变得不稳定的临界荷载,其中修正的牛顿-拉普森(下文简称为 NR 方法)是最常用的非线
性求解方法。
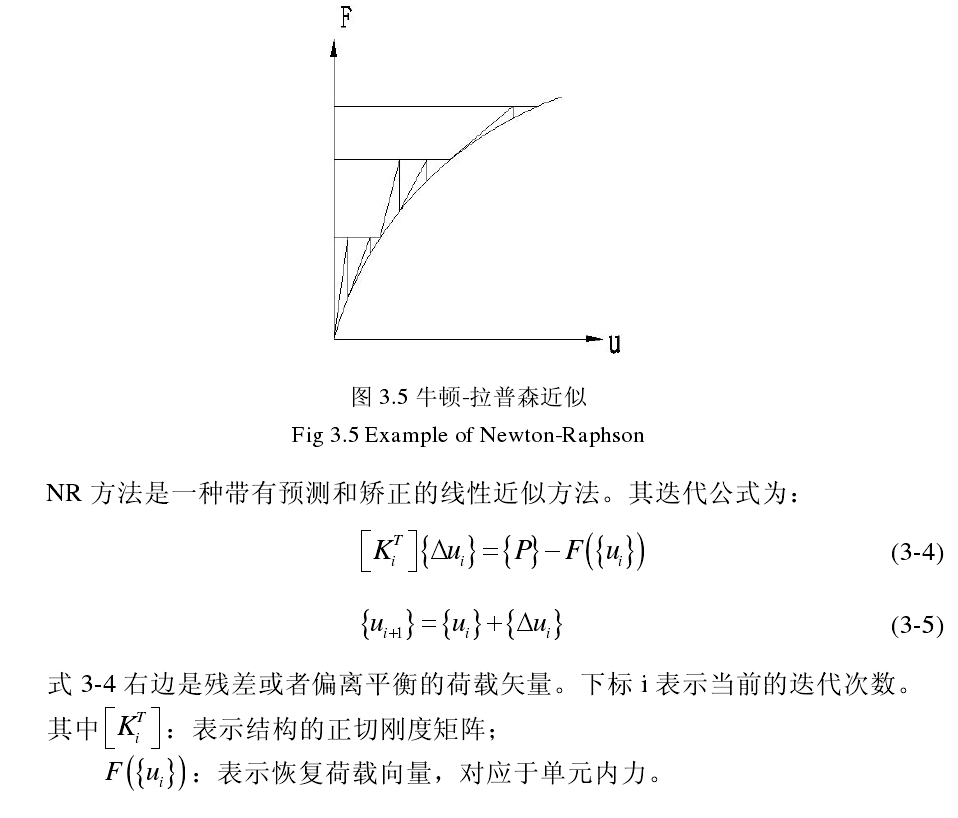
ANSYS 程序中 NR 方法[
23]包括全牛顿-拉普森方法(Full Newton-Raphson)、修正牛顿-拉普森方法(Modified Newton-Raphson)及拟牛顿-拉普森迭代法(Quasi Newton-Raphson)。
①全牛顿-拉普森方法
这种方法每进行一次平衡迭代就要修改一次刚度矩阵,如果打开了自适应下降,只要迭代残余项减小,程序将仅使用正切刚度矩阵,如果自适应是关闭的程序每一次平衡迭代都使用正切刚度矩阵;全牛顿-拉普森方法对于复杂的非线性问题有良好的收敛能力。
②修正牛顿-拉普森方法
在修正的牛顿-拉普森方法中系统在每一个子步都会对正切刚度矩阵进行修正,但是在迭代过程中不修正刚度矩阵,即每个荷载子步仅生成一次刚度矩阵。修正的牛顿-拉普森方法不适用于大变形分析。
③拟牛顿-拉普森迭代方法与修正的牛顿-拉普森法的区别在于拟牛顿-拉普森能通过修改残差来提高收敛速度。
ANSYS 程序提供了一系列帮助收敛的方法,如线性搜索,自动荷载步长,当不能得到收敛时程序会尝试减小荷载增量来求解。但是对于某些非线性问题,仅仅使用 NR 方法,在处理可能变为降秩矩阵的正切刚度矩阵时可能会遇到严重的问题。包括结构突然崩溃或者突然跃越至另一种平衡状态等。

 扫一扫,关注我们最新消息
扫一扫,关注我们最新消息