稳定分析的有限元方法
有限元法是现代工程计算中使用最广泛的数值方法,由于其通用性和有效性,受到工程技术研究人员的重视。特别是近年来,随着计算机计算能力的提升,有限元广泛应用与航天、船舶、海洋、机械、土木等领域。有限元软件中 ANSYS 是使用最广泛的商用软件之一。该软件不但能进行线性屈曲分析,也具备强大的非
线性计算能力。本文也采用 ANSYS 进行线性和非线性分析。
有限单元法的基本思想是将结构离散化,从而将实际结构简化为有限个单元的组合。通过对离散后的模型进行分析可以得到满足工程应用进度的实际结构的力学性能。正是因为有限单元法将本来无限个自由度的实际结构简化为有限个自由度,通过更加细致的单元划分,可以使得离散的单元在模型精度、边界条件等各方面不断接近实际结构。
线性稳定分析
有限单元法的线性稳定分析其实是对结构刚度矩阵的特征值分析[21, 23]。可以用来计算理想弹性结构的理论屈曲荷载。
考虑到轴向力和薄膜力在弯曲中的抵抗效应,需要考虑几何刚度矩阵。 在计算结构特征值时,将结构划分为个数有限的单元,形成结构的弹性刚度矩阵[KE],并且考虑结构几何刚度矩阵[KG]。结构的平衡方程即可写为:
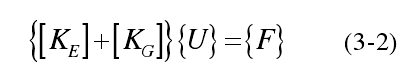
式中,{U}为节点位移向量,{F}为总的横向节点载荷向量。式(3-6)也是非线性分析的平衡方程。为了得到结构的其他平衡状态,根据势能驻值原理应该使系统的总势能二阶变分为零,即:
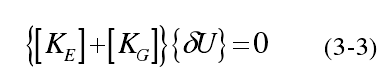

在进行特征值屈曲分析的时候,需要注意:
①由于特征值分析不考虑任何非线性和初始缺陷,因此只能产生非保守的结果,且通常情况下都会过高估计结构的临界荷载,通常不能用来指导工程实践;
②由特征值方程求解得到的特征值都表示为初始荷载{P0}的比例因子,因此在进行线性屈曲分析的时候只需要施加一个很小的单位荷载;
③不允许非线性行为;在模型中如果采用了非线性单元,ANSYS 都只进行线性处理,而忽略其非线性特性;
另一方面,特征值屈曲计算速度很快,大多数时候在进行非线性屈曲分析之前,都需要进行特征值分析以了解结构的屈曲形态。
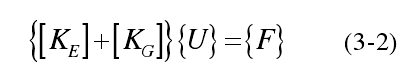
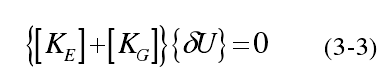

 扫一扫,关注我们最新消息
扫一扫,关注我们最新消息