由前面稳定问题的分类可以得知,结构处于平衡状态时并不一定就是稳定的。比较经典的例子是一个处于不同平衡位置的小钢球,如下图 3.4,虽然三个图中的小钢球都处于平衡状态,但是其稳定性就完全不同了。对 a 图中的小球施加轻微扰动,小球会暂时偏离平衡点,但是在扰动撤去后小球可以顺利回到初始的平衡
位置,这种平衡状态就是稳定的。图 b 中的小球在受到轻微扰动后离开初始位置,在扰动撤去后,并不能回到初始位置,而是停留在这个新的位置继续保持平衡,这种平衡状态被称为随遇平衡。图 c 中的小球在受到轻微扰动后,其势能降低,在扰动撤去后不能回到初始位置,反而继续偏离初始平衡位置,这种平衡便是不
稳定平衡。
对于不同的平衡状态,需要以数值或者理论方法来判别一个结构处在的平衡状态是否稳定,稳定问题的计算方法主要分为静力平衡法、能量法(铁木辛柯法)、缺陷法、动力法。 在这几种经典方法中,平衡法和缺陷法能处理一些简单问题的精确解,但是仅能求解屈曲荷载不能判断结构的稳定状态;能量法既能求解精确解和屈曲荷载,也能判断结构屈曲后的稳定状态,并且能量法适合求解复杂问题的数值近似解。以上这三种方法都属于静力问题,只能适用于保守系统。振动法由动力学观点出发,能适用于非保守系统。由于其使用了偏微分方程来描述系统的运动,在求解上会有很大的数学困难。
在有限单元法中能量准则的适用性最好[23],能量法认为在承受保守力的结构中,可以根据已变形结构的受力情况建立总势能,总势能是结构应变能和外力势能之和。结构若处于平衡状态,总势能就有驻值,根据势能驻值原理,由总势能对位移的一阶变分=0,就可以得到平衡方程,再由平衡方程求解分岔屈曲荷
载。而要判断结构的稳定性能则需要对总势能进行二阶甚至更高阶变分进行研究。
当结构处于平衡状态附近受到轻微扰动时,结构的总势能产生增量
由于结构处于平衡,根据虚功原理总势能的一阶变分=0,如果结构总势能的二阶变分20,则总势能增量 0即总势能处于极小值,结构的平衡状态是稳定的平衡状态,例如前面例子中的第一个小球。当结构的二阶变分小于零,总势能增量小于零,此时结构的稳定状态就是不稳定的状态。当结构的二阶变分
为零,结构则处于从稳定的平衡状态向不稳定的平衡状态过度的临界状态,例如前面例子中的第二个小球,此时要研究结构的稳定性就需要对总势能的三阶四阶甚至更高阶的变分。
失稳的原因
关于失稳的原因,文献[26]以受压杆为例做了如下解释:按照能量理论,细长杆在轴向压力作用下会缩短,此时荷载的势能转化为结构的应变能,势能降低,从这方面可以得出荷载的势能要降低这个基本规律;物理现象会按照最容易的线路发生,这是第二个基本规律。对轴压杆而言,要使荷载的势能降低有多种变形方式,例如轴向压缩或者弯曲失稳。当荷载较小的时候,柱子会采用轴向缩短的方式来降低荷载的势能;当荷载超过某一数值时,柱子会选择以弯曲的方式来使荷载的势能降低。按照之前的两个基本规律,柱子在选择是缩短使势能降低还是弯曲使荷载降低这两种方法的时候,比较的标准就是这两个方法的容易程度。即在荷载达到一定程度后,柱子采用弯曲的方式使势能降低,是较压缩而言更加容易的路径。
在现代结构的发展趋势上,由于高强度材料和更加优秀的结构形式的采用,结构向着横向更大跨度,竖向更高的趋势发展。在经济性的要求下,结构的截面尺寸越来越小而跨度高度越来越大,这就导致了稳定问题的发生 
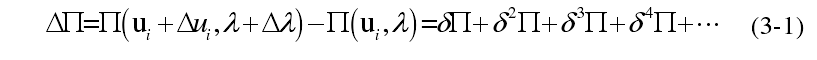
 扫一扫,关注我们最新消息
扫一扫,关注我们最新消息