有限单元法中计算结构处于某状态下的振型和频率,需要建立运动方程,其中包括几何刚度的平衡方程[23]为:
由式 2-2,可以得出结构的有效刚度与结构的应力状态相关,振型和对应频率也与应力状态有关,例如一根张紧的弦的频率会随着张紧力的大小变化而变化。
不同工况下的模态分析
由于活塞的质量占整体结构重量的一半以上,且活塞的刚度很大[12],在结构的动力特性分析中,需要正确地处理活塞与柜体的关系,才能准确地计算出结构的动力特性。本文的分析中,建立了活塞的实体模型,对空桶、活塞处于低位、活塞处于中位、活塞处于高位这四种工况进行了分析。
①空桶状态下的模态
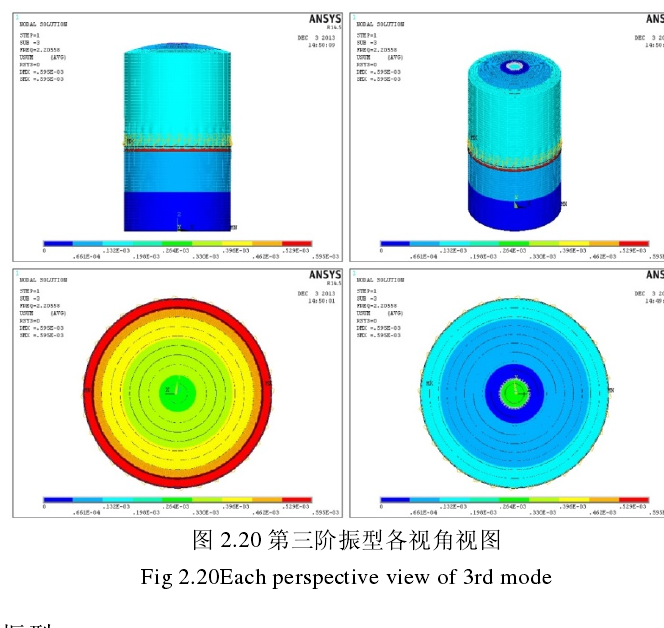
1)第一振型
频率:2.324s-
1,周期:0.430s。形态为“柜体四瓣呼吸,柜顶不动”,为主模
态(The driven mode),第二阶振型为其伴随模态(The companion mode),形态相似仅
但旋转了/
(2n),m=1,n=4,其中 n 为环向波数,m 为纵向半波数。
2)第三振型
频率:2.556s-1,周期:0.391s。形态为“柜体三瓣呼吸,柜顶不动”,为主模 15 态,第四阶振型为其伴随模态,形态相似仅角度旋转了/(2n),m=1,n=3。
图 2.14 第三阶振型各视角视图
Fig 2.14Each perspective view of 3nd mode
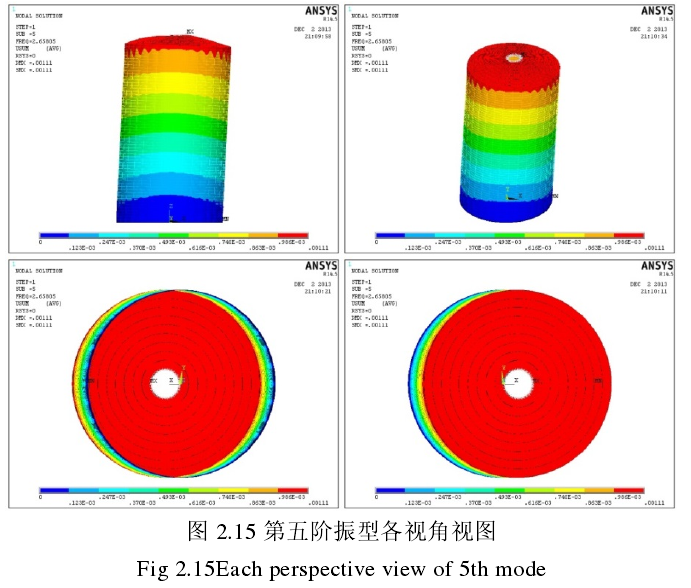
3)第五振型
频率:2.658s-
1,周期:0.376s。形态为“柜体摆头”,为主模态,第六阶
3)第五振型
频率:2.658s-
1,周期:0.376s。形态为“柜体摆头”,为主模态,第六阶振型为其伴随模态,形态相似仅角度旋转了π/(2n),m=1,n=1。
15
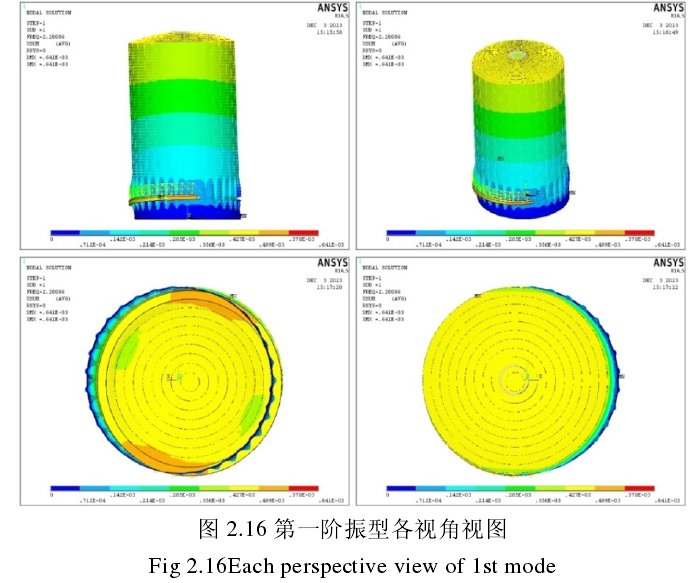
第二阶振型为其伴随模态,形态相似仅角度旋转了/(2n),m=1,n=1。
π
图 2.16 第一阶振型各视角视图
Fig 2.16Each perspective view of 1st mode
2)第三振型
频率:2.437s-
1,周期:0.410s。形态为“活塞旋转,支架变形”。
图 2.17 第三阶振型各视角视图
Fig 2.17Each perspective view of 3rd mode
3)第四振型
频率:2.462s-
1,周期:0.406s。形态为“柜体四瓣呼吸,柜顶不动
频率:2.462s-
1,周期:0.406s。形态为“柜体四瓣呼吸,柜顶不动”,为主模
态,第五阶振型为其伴随模态,形态相似仅角度旋转了/
(2n),m=1,n=4。
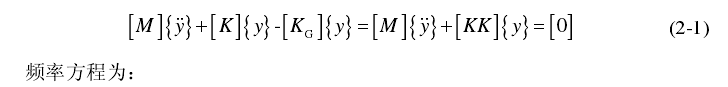

 π
π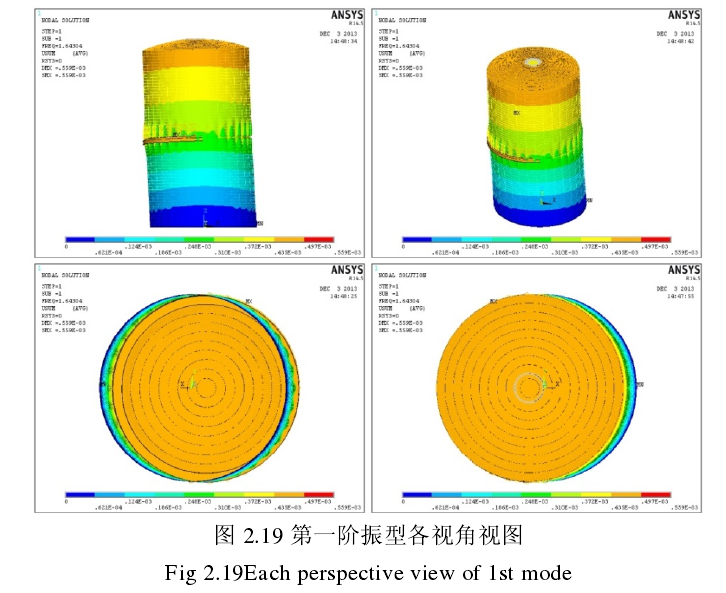
 扫一扫,关注我们最新消息
扫一扫,关注我们最新消息